Esta es una continuación del trabajo titulado
Relaciones entre la música y las matemáticas
realizado y publicado por la Universidad de Valladolid
La notación modal y los modelos rítmicos
Como la polifonía medieval se iba haciendo cada vez más y más compleja, los compositores tenían que encontrar algún medio de indicar cómo encajaban las voces y los sonidos de los instrumentos musicales.
Lo que necesitaban era un sistema de notación que mostrara los valores relativos de las notas dentro de una única línea melódica. El desarrollo de ese sistema, fue una de las realizaciones más significativas de la escuela de Notre Dame.
Relaciones entre sonidos
En la música es muy importante la relación que existe entre la frecuencia de los distintos sonidos, a esta relación se le llama intervalo. Los intervalos musicales pueden medirse en términos de la relación de frecuencias de los sonidos, aunque en música reciben nombres propios cuya correspondencia física depende del tipo de escala utilizada.
Los más importantes, por su simplicidad y su importancia a la hora de construir la escala musical, son:
-
La octava. Cuando la cuerda medía un medio del total, el sonido se repetía, pero más agudo. La octava es lo que correspondería a un salto de ocho teclas blancas del piano; o mejor dicho, una octava es la repetición de un sonido con una cuerda con la mitad de longitud, por tanto, otra nota armoniosa. Su frecuencia es doble.
-
La quinta es otro intervalo entre notas que se obtiene con una cuerda de largura dos tercios de la inicial. Su frecuencia es de tres medios del sonido inicial. Corresponde a un salto de cinco teclas blancas en un piano.
-
La cuarta es, como las anteriores, otro intervalo entre notas que se obtiene con una cuerda de largura tres cuartos de la inicial. Su frecuencia es cuatro tercios de la nota inicial.
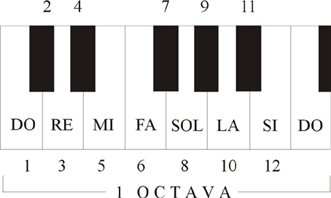
El siguiente esquema muestra un fragmento del teclado de piano, a cada tecla le corresponde una nota musical. La última columna indica la frecuencia correspondiente (en Hertz):
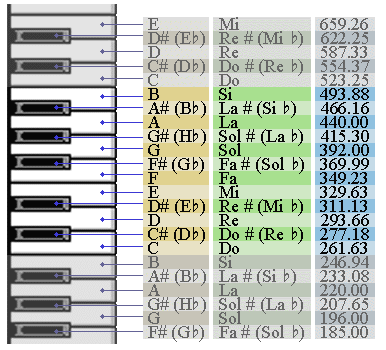
En este esquema se puede ver que las teclas forman grupos de 12 (7 blancas y 5 negras), y estos grupos se repiten de izquierda a derecha. Cada octava tecla blanca cierra un grupo y abre el otro, y por eso la distancia musical entre esas teclas se llama octava (normalmente se llama octava también el mismo grupo de 12 teclas), y su escala es igual a 2:1 – esto es, la frecuencia de la misma nota de siguiente octava es el doble, y la de octava anterior es la mitad. La distancia de dos octavas le corresponde a la relación de frecuencias de 4:1, tres octavas – 8:1 etc.: para sumar distancias tenemos que multiplicar las relaciones de frecuencias. La nota “La” (o “A”) es la nota de etalón – su frecuencia es 440 Hz.
Así a partir de un sonido original obtenemos diferentes notas armoniosas. Haciendo un pequeño esquema nos aclararemos mejor:
|
Nota |
Frecuencia |
Long. cuerda |
|
Original |
F |
L |
|
Octava justa |
2f |
(1/2)L |
|
Quinta mayor |
(3/2)f |
(2/3)L |
|
Cuarta justa |
(4/3)f |
(3/4)L |
|
Tercera mayor |
(5/4)f |
(4/5)L |
|
Tercera menor |
(6/5)f |
(5/6)L |
si suponemos que la nota inicial es el do, entonces, la octava, quinta y cuarta son las notas:
|
Nota base |
Cuarta |
Quinta |
Octava |
|
Do |
Fa |
Sol |
Do (1 octava más alta) |
que corresponden a la cuarta, quinta y octava notas respectivamente de la escala diatónica (las teclas blancas del piano), que veremos un poco más adelante.
Esta ordenación de los sonidos musicales ha sido fruto de un largo proceso. Desde la elección de un sonido base, a partir del cual construir el resto, a la determinación del intervalo que hay entre una nota y la siguiente.
Así, una escala es una serie de notas ordenadas de forma ascendente o descendente, donde a la primera de las notas se la llama tónica.
Escala musical occidental (actual)
Se llama escala musical a la sucesión de sonidos constitutivos de un sistema (tonalidad) que se suceden regularmente en sentido ascendente o descendente, y todos ellos con relación a una nota que da nombre a la escala, o tónica.
La sucesión de sonidos en una escala es por movimiento conjunto, y se hace según las leyes de la tonalidad.

El origen de la escala musical
La escala actual (escala occidental) es el resultado de un largo proceso de aprendizaje de las notas. Los pitagóricos construyeron un aparato llamado monocordio que se componía de una tabla, una cuerda tensa y una tabla más pequeña que se iba moviendo por la grande.
La construcción de la escala musical
La escala diatónica es la formación de una escala a partir de las distancias de tono y semitono. Son las más conocidas y usadas y la mayoría de ellas están formadas por siete notas, pero las hay también de seis u ocho.
Ordenadas las notas así: do, re, mi, fa, sol, la, si, y al añadirle un octavo sonido, de nuevo do, hemos formado una escala diatónica:
|
I
|
II |
III |
IV |
V |
VI |
VII |
VIII |
|
do |
re |
mi |
fa |
sol |
la |
si |
do |
Pero, ¿cómo se pueden encontrar las notas de nuestra escala musical a partir de una nota base (tónica)?. Se puede hacer un proceso repetitivo a partir de esta nota, utilizando las quintas y las octavas:
Lo que queremos hacer es encontrar notas armoniosas con la nota base que se encuentren entre la nota original y su octava.
-
Supondremos que la nota original tiene una frecuencia f. Entonces, la octava tendrá frecuencia 2f. Queremos encontrar notas que tengan frecuencia entre f y 2f.
-
La primera que tenemos es la quinta, la frecuencia es (3/2)*f. Corresponde a una cuerda de longitud 2/3 la inicial.
-
El siguiente paso es encontrar la quinta de la quinta. La frecuencia será (3/2)*(3/2)*f=(9/4)*f. El problema es que esa nota tiene una frecuencia más grande que 2f. Lo que hacemos es encontrar una nota una octava más abajo. Es decir, una nota con frecuencia (9/8)*f.
Si vamos repitiendo el proceso obtenemos las notas siguientes:
– f
– (3/2)*f
– (9/8)*f. Después de haber descendido una octava.
– (3/2)*(9/8)*f = (27/16)*f
– (3/2)*(27/16)*f = (81/32)*f. Como la frecuencia es más grande que 2f, descendemos una octava y obtenemos (81/64)*f
– (3/2)*(81/64)*f = (243/128)*f
Hemos obtenido 7 notas, contando la octava, que podemos ordenar de frecuencia más pequeña a más grande de la forma siguiente:
|
Nota
Base |
f |
|
9/8·f |
|
|
81/64 ·f |
|
|
Quinta |
3/2·f |
|
27/16·f |
|
|
243/128·f |
|
|
Octava |
2·f |
De esta forma hemos obtenido 6 notas dentro de una octava. Pero si nos fijamos en la razón de frecuencias de una nota y la anterior, parece que hay un agujero entre (81/64)*f y (3/2)*f. Curiosamente entre estos dos valores se encuentra (4/3)*f, que corresponde a lo que hemos llamado cuarta.
|
(9/8):1=9/8 |
1,125 |
|
(81/64):(9/8)=9/8 |
1,125 |
|
(3/2):(81/64)=32/27 |
1,185 |
|
(27/16):(3/2)=9/8 |
1,125 |
|
(243/128):(27/16)=9/8 |
1,125 |
|
2:(243/128)=256/243 |
1,053 |
Añadiendo la cuarta, nos queda una escala de 7 notas con estas razones entre las frecuencias: (en la columna de la derecha hemos puesto el nombre de la nota que correspondería si la nota base fuese el do):
|
Frecuencia |
Razón nota anterior |
||
|
Tónica |
F |
Do |
|
|
Segunda |
9/8·f |
9/8=1,125 |
Re |
|
Tercera |
81/64·f |
9/8=1,125 |
Mi |
|
Cuarta |
4/3·f |
256/243=1,053 |
Fa |
|
Quinta |
3/2·f |
9/8=1,125 |
Sol |
|
Sexta |
27/16·f |
9/8=1,125 |
La |
|
Séptima |
243/128·f |
9/8=1,125 |
Si |
|
Octava |
2f |
256/243=1,053 |
Do |
Estas son las 7 notas de la escala diatónica (que se corresponden a las teclas blancas del piano), la octava es la misma que la anterior una octava más alta. De cualquier forma, en una octava se utilizan 12 notas. Las 5 notas restantes se simbolizan añadiendo a la derecha el carácter # (sostenido) o b (bemol).
Podemos ver que hay dos razones diferentes: el tono 9/8 y el semitono 256/243. La pregunta que nos hacemos es qué relación hay entre las dos razones. Se puede ver que dos semitonos hacen casi un tono (256/243)2 =1,109, pero no es exactamente el mismo.
Si ahora utilizásemos las cuartas para ir encontrando nuevas notas armoniosas, comenzarían a salir las “teclas negras” del piano, es decir, los sostenidos y los bemoles. Cuando la escala queda completa con 12 notas (las teclas negras y las blancas), esto es lo que se llama la escala cromática .
El pentagrama
En música la representación gráfica de los sonidos se hace por medio de unos símbolos (las notas), que se escriben sobre una pauta llamada pentagrama. El pentagrama es una manera de realizar una notación musical de tal modo que la misma sea fácilmente transmisible a otras personas. Esto significa que así como las letras del alfabeto se juntan para formar una frase, de la misma manera los símbolos musicales se juntan en el pentagrama para formar una canción que puede ser interpretada por un instrumento musical o cantada por la voz del ser humano.
Un típico pentagrama en clave de Sol:

Básicamente los pentagramas están formados por un conjunto de cinco líneas dispuestas de forma paralela. A la izquierda del conjunto de líneas aparece un símbolo distintivo llamado “clave”. Esta clave es la que determinará a qué nota musical corresponde cada uno de los símbolos musicales que aparecen en el pentagrama. En el gráfico anterior encontramos un símbolo que identifica a la “clave de Sol”: ![]() . Existe una variedad considerable de claves en otras notas como Do y Fa , por ejemplo. Como vemos a continuación, el símbolo de laclave de Fa es:
. Existe una variedad considerable de claves en otras notas como Do y Fa , por ejemplo. Como vemos a continuación, el símbolo de laclave de Fa es: ![]()
Un pentagrama en clave de Fa:

La interpretación del pentagrama
Las notas musicales que aparecen dentro del pentagrama pueden colocarse justo encima de alguna de las líneas o en los espacios entre las mismas. Según la clave que corresponda (Sol, Do, Fa, etc.) y la ubicación específica entre las líneas, cada símbolo musical nos brindará información sobre una única nota. La duración en el tiempo de la misma vendrá dada por las características del símbolo musical utilizado.
La nota, gracias a su aspecto y su posición, permite definir simultáneamente tres parámetros:
– La posición vertical de la nota define su altura (aguda o grave). Cuanto más arriba se sitúe la nota sobre las líneas o los espacios del pentagrama, más aguda será.
– La posición horizontal de la nota define cuando es emitida. Así, el eje horizontal del pentagrama define una escala de tiempo creciente desde la izquierda hacia la derecha. Si existiesen dos notas en la misma columna, estarían emitidas simultáneamente.
– La forma de la nota define su duración. Duraciones estándar de notas están definidas en solfeo; cada una es dos veces más corta que la siguiente. Así, se tiene:
La redonda ![]() , blanca
, blanca ![]() , negra
, negra ![]() , corchea
, corchea ![]() , semicorchea
, semicorchea ![]() , fusa
, fusa ![]() , etc.
, etc.
Así, una blanca es dos veces más corta que una redonda, una negra dos veces más corta que una blanca…
La escala temperada
Como un tono no es exactamente dos semitonos, había lugares donde los intervalos eran más grandes o más pequeños que en otros lugares. Esto daba problemas para afinar instrumentos con intervalos fijos como el piano o la guitarra. Es para esto que se creó la escala temperada.
El temperamento es la forma musical de mantener series dentro de un espacio definido. La transición de la afinación pitagórica a la temperada tomó siglos, y ocurrió de una manera paralela al cambio en la relación entre música y matemáticas.
En el siglo XII, compositores e intérpretes el querer separarse de la tradición pitagórica crearon nuevos estilos y tipos de música como el canto monódico gregoriano que poco a poco fue evolucionando en música polifónica con diferentes instrumentos y voces.
La creación de composiciones más complejas llevó a experimentar con afinaciones alternativas y temperamentos; los experimentos de afinación derivaron en un cambio de la afinación pitagórica llamada la afinación justa. Las nuevas afinaciones seguían utilizando las matemáticas para calcular los intervalos, pero no necesariamente seguían los principios pitagóricos. Ahora eran utilizadas de una forma práctica y no como un fin; este cambio de actitud causó desacuerdo entre los matemáticos, quienes querían una adherencia estricta a sus fórmulas, y los músicos que buscaban reglas fáciles de aplicar. De hecho, los músicos empezaron a basarse más en su oído y menos en el monocordio.
En el siglo XVIII, músicos como Juan Sebastián Bach empezar a afinar sus instrumentos usando el temperamento, es decir, una escala en la que los doce sonidos fueran afinados sin diferencia entre un fa sostenido y un sol bemol. La complejidad de las modulaciones lo necesitaba.
Juan Sebastian Bach compuso el clave bien temperado, que consiste en 24 piezas en las doce tonalidades, usando el modo mayor y menor de cada una de ellas, demostrando de esta manera las posibilidades de modulación creadas por una afinación igual.
La cantidad de notas que tiene esta escala es la misma, pero la forma de afinación es diferente. En la escala temperada, la razón entre la frecuencia de una nota y la anterior es siempre constante.
Si llamamos r a esta razón, se cumplirá que las frecuencias formaran una progresión geométrica del tipo:
f, f·r, f· r2, f·r3, f·r4, …, f·r12 = 2·f
de lo que se deduce que r12 = 2, de donde r =![]() = 1,059…
= 1,059…
Esta escala resuelve los problemas de afinación, pero no podemos olvidar que las notas más armoniosas eran las que se había encontrado mediante el método geométrico, es decir las de la escala cromática. Instrumentos sin intervalos fijos como violines, contrabajos, etc. pueden utilizar la afinación de la escala cromática.
La escala natural
El oído humano tiene una “construcción” tal, que los sonidos cuyas frecuencias están en la proporción simple (2/1, 3/2, 4/3 etc), suenan juntos de una manera agradable. Por otro lado, casi todos los procesos físicos que producen sonidos, además de la frecuencia principal (o el tono básico) producen también “armónicas”, es decir, las frecuencias que son dos, tres, cuatro -una cantidad entera- veces más altas. El conjunto de las armónicas constituye el timbre que es único para cada instrumento musical.
Escogeremos como base la frecuencia de 55 Hertz (esta frecuencia es absolutamente arbitraria, la única razón es que nos lleve a la frecuencia 440 Hertz que es un etalón musical contemporáneo) y vamos a multiplicarla por 2, 3, 4, etc. Obtendremos la siguiente serie:
55; 110, 165; 220, 275, 330, 385; 440, 495, 550, 605, 660, 715, 770, 825; 880
Colocaremos estas frecuencias en sus octavas correspondientes, y arreglaremos la serie en forma de una tabla:
|
Octava 1 |
55 |
|||||||
|
Octava 2 |
110 |
165 |
||||||
|
Octava 3 |
220 |
275 |
330 |
385 |
||||
|
Octava 4 |
440 |
495 |
550 |
605 |
660 |
715 |
770 |
825 |
|
Octava 5 |
880 |
|||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
Observamos que la segunda octava tiene dos notas, la tercera – cuatro, y la cuarta – ocho, eso es, ¡una octava completa natural! Ahora vamos a calcular las distancias entre las notas:
|
440 |
8:9 |
495 |
9:10 |
550 |
10:11 |
605 |
11:12 |
660 |
| A4 | B4 | C5 | D5 | E5 | ||||
| 1:1 | 9:8 | 5:4 | 11:8 | 3:2 |
| 12:13 |
715 |
13:14 |
770 |
14:15 |
825 |
15:16 | 880 |
| F5 | G5 | H5 | A5 | ||||
| 13:8 | 7:4 | 15:8 | 2:1 |
En las celdas superiores intermedias se indica las distancias entre las frecuencias vecinas, y en las celdas inferiores, las distancias con respeto a la frecuencia principal, que en nuestro ejemplo es 440 Hz. La numeración de octavas (4-a o 5-a) corresponde al estándard contemporáneo.
El producto de todas las relaciones intermedias es igual a 2, esto es, a una octava. La serie ordenada de esta manera se conoce como escala. La escala que acabamos de construir se conoce como escala natural.
La distancia musical entre la nota principal y la segunda armónica es 2/1 – una octava. La distancia musical entre la segunda y la tercera armónica en la música se llama quinta, le corresponde la relacion de frecuencias 3/2. En nuestra escala es la distancia entre las notas A4 y E5. La distancia entre la 3-a y 4-a armónica es cuarta -con la relación 4/3-, como entre las notas E5 y A5. Estos son distancias o intervalos fundamentales en la música.
Leer artículos anteriores: Click Aquí

